Derivative of 1/x Formula
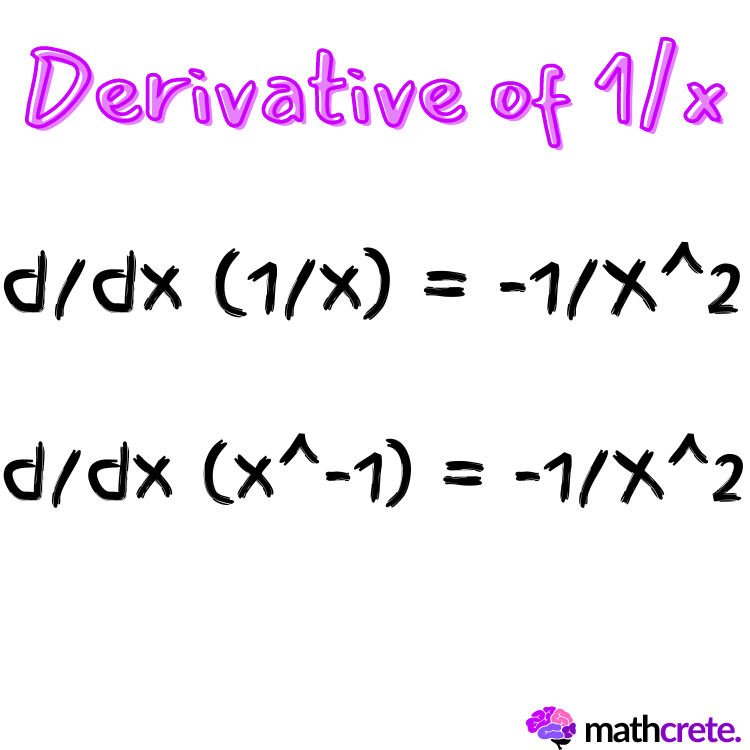
The derivative of $\frac{1}{x}$ is equal to $ \frac{d}{dx} (\frac{1}{x})=-\frac{1}{x^2}$.
Rewriting 1/x using the negative exponent rule, we get $x^{-1}$ which also has the same derivative $ \frac{d}{dx} (x^-1)=-\frac{1}{x^2}$.
As a common derivative, there are many ways we can obtain the derivative of 1/x, either by using the basic principles of limits, or using the power rule in derivatives.
So, let’s find and show the differentiation of 1/x using both methods!
Finding the Derivative of 1/x Using Power Rule
Recall that the power rule of derivative in Calculus states that if $x$ is a variable and there is an $n$ power $x^n$, then the derivative of $x$ raised to the power $n$ can be written as $f’(x)=\frac{dy}{dx} (x^n) = nx^{n-1}$ for any $n$ not equal to 0.
Now let’s find the derivative of $\frac{1}{x}$ using the power rule.
1. Rewrite $\frac{1}{x}$ into an exponential form. We came up with a negative exponent since it shows that the base is on the denominator of the fraction line $\frac{1}{x}$ – that’s based on the negative exponent rule.
$f(x)=\frac{1}{x}$
$f(x)=x^-1$
2. Differentiate both sides with respect to variable x using the power rule. Following the formula $f’(x)=\frac{d}{dx} (x^n) = nx^{n-1} $, the value of $n$ will be -1.
$f(x)=x^-1$
$f’(x)=\frac{d}{dx}=(-1)x^{(-1-1)}$
$f’(x)=\frac{d}{dx}=-\frac{1}{x^2}$
Finally, the answer to the derivative of 1/x using the power rule is $-\frac{1}{x^2}$.
Finding the Derivative of 1/x Using First Principles/Limit Definition
Let us recall that the first principle of a derivative of a function $f(x)$ is given by the limit $f'(x)=\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}$. Simply plug in $\frac{1}{x}$ to $f(x)$ and $\frac{1}{x+h}$ to $f(x+h)$.
$f'(x)=\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}\\$
$f'(x)=\lim_{h \rightarrow 0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}\\$
$f'(x)=\lim_{h \rightarrow 0}\frac{\frac{x}{x(x+h)}-\frac{x+h}{x(x+h)}}{h}\\$
$f'(x)=\lim_{h \rightarrow 0}-\frac{\frac{h}{x(x+h)}}{h}\\$
$f'(x)=\lim_{h \rightarrow 0}-\frac{h}{x(x+h)}*\frac{1}{h}\\$
$f'(x)=\lim_{h \rightarrow 0}-\frac{1}{x^2+hx}\\$
$f'(x)=-\frac{1}{x^2}$
Thus, using the first principle of derivatives, the derivative of $\frac{1}{x}$ is equal to $-\frac{1}{x^2}$.
What Is the Derivative of 1/x^2?
The form $\frac{1}{x^2}$ is the same with $\frac{1}{\sqrt{x}}$. The derivative of $x$ raised to the power $n$ can be we written as $f’(x)=\frac{dy}{dx} (x^n) = nx^{n-1}$ for any $n$ not equal to 0. Now let’s find the derivative of $\frac{1}{x^2}$ using the power rule.
1. Rewrite $\frac{1}{x^2}$ into an exponential form. We came up with a negative exponent since it shows that the base is on the denominator of the fraction line $\frac{1}{x^2}$ – that’s based on the negative exponent rule.
$f(x)=\frac{1}{x^2}$
$f(x)=x^-2$
2. Differentiate both sides with respect to variable x using the power rule. Following the formula $f’(x)=\frac{d}{dx} (x^n) = nx^{n-1} $, the value of $n$ will be -1.
$f(x)=x^-2$
$f’(x)=\frac{d}{dx}=(-2)x^{(-2-1)}$
$f’(x)=\frac{d}{dx}=-\frac{2}{x^3}$
Finally, the final answer to the derivative of 1/x^2 using the power rule is $-\frac{2}{x^3}$.

Generally I don’t read article on blogs, however I wish to say that this write-up
very compelled me to check out and do it! Your writing style has been amazed me.
Thank you, quite nice post.